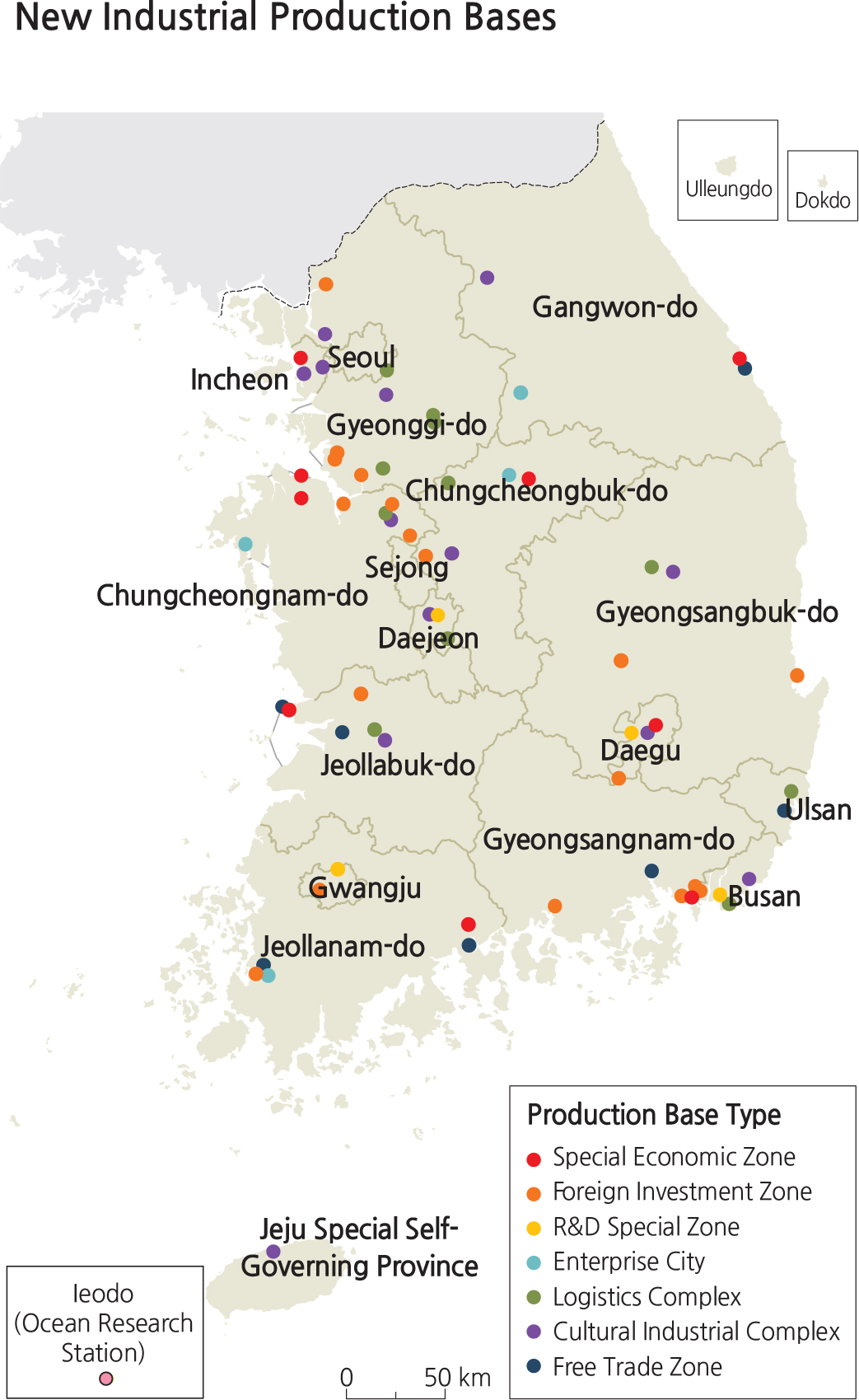
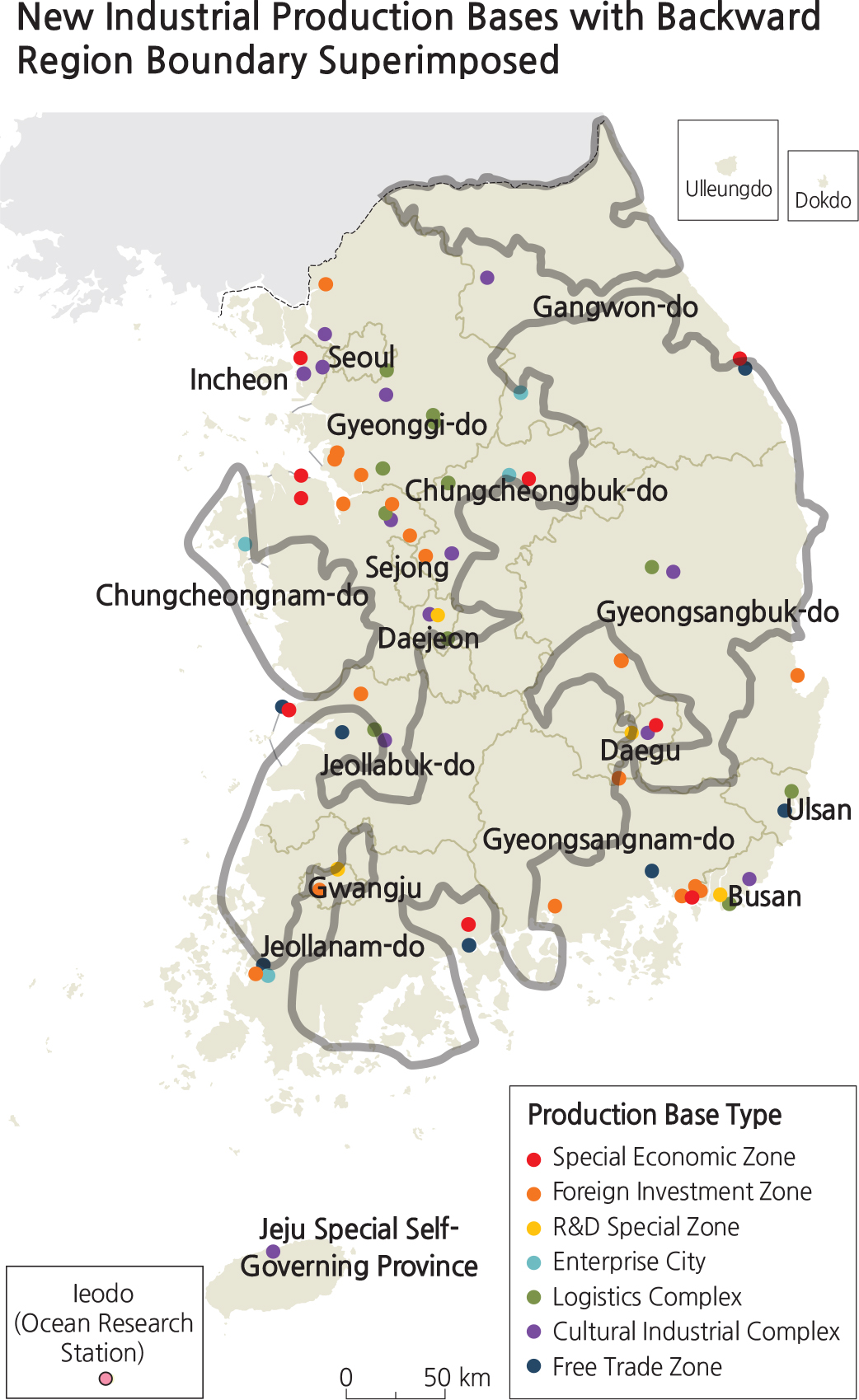
As can be imagined, not all map data are created equal. In order to evaluate the accuracy of a map, it is helpful to have a better understanding of the nature of map data. Map data can be classified by several different categories that have very different real and visual characters, as follows:
•By dimensions: point data has no dimension, but each point occupies a location; line data are considered onedimensional; area data are two-dimensional; volumetric data are three-dimensional; volumetric data through time can be considered four-dimensional.
•By time-frame (or temporality): temporal data are considered historic or something that happened in an instant in the past, and they can be dated or out-dated; real-time data (such as continuous satellite scans of the earth) are as current as can be. When a map is made, it is important for the cartographer to provide a clue as to when the data were captured and then mapped (either in the map title or in the map legend).
•By spatial aspects: spatial data or geographic data specifically define the location of data points (e.g., GPS locations, latitude and longitude descriptions); nonspatial data include attribute data or thematic data about a geographic feature (e.g., all the wells in La Crosse County, Wisconsin can be located as spatial data, while the degree of contamination of the water taken from each well is a set of thematic data). By putting locations with water contamination data, a map can be made of the overall spatial pattern of contaminated water for the whole county.
•By continuity: data can be discrete (countable in whole numbers), such as one house, two houses. Data can also be continuous, such as with time or population density. For example, the number of persons divided by the area of a geographic entity might be 356.23451083 persons per square mile; notice that this particular number is carried out to 8 digits beyond the decimal. Chances are it can be more
than 8 digits; however, in the map legend, it is normally rounded off as 356 or placed in a category of 300-400 persons per square mile. Regardless, such a number is still continuous data.
•By numerical aspects: quantitative data refer to actual numbers in a dataset (e.g., a population density map is a quantitative map showing higher and lower densities). Qualitative data refer to things that are not described numerically (e.g., a geologic map is considered a qualitative map because it shows all different types of geology without the use of numbers). Other qualitative map examples are planning maps (where to locate dams, transportation routes, electricity generating plants, etc.; an example is the National Territorial Planning Map on p. 77 of the National Atlas of Korea I).
•By appearance: Concrete data refer to things that can be seen and directly enumerated, such as an urban land use setting that delineates which parts of the city are devoted to greenways or commerce or residential or industrial land use—ll of which are easily observable objects. Abstract data are things that one cannot generally see, such as population density or barometric pressure patterns. These things may have to be calculated or measured with instruments.
•By origin: observed data refer to data that are enumerated or collected by field methods or with the use of instruments. Derived data are those that are calculated or computed, for example, taking the population of Greater New York City (available from the Census Bureau) and dividing it by the area of Greater New York City (based on ground surveys) results in derived data in the form of population density.
•By measurements: these refer to nominal data, ordinal data, interval data, and ratio data. Nominal data refers to named information like a house, a light house, or a dam, and so on; these data are qualitative and do not possess any rankings because they are individual geographic entities. Ordinal data refer to data that have a ranking but no specific numerical certainties. For example, with a map showing areas of low, medium, or high crime rates in a city, the reader may not know precisely what is considered low, medium, or high, or the thresholds of these categories. Other rank order examples are: hot-warm-cool-cold, or dense-medium-sparse. Interval data refers to assigned numeric data values but with no baseline for comparison. For example, water freezes at 32° F and boils at 212°F but at the same time it can be measured in Centigrade for the same coldness or hotness at 0°C for freezing or 100°C for boiling. There is no baseline for comparing the degree of coldness or hotness between Fahrenheit and Centigrade. Ratio data provide a baseline for comparison; the 1 on the left side of the ratio sets the standard for comparison; thus, a scale of 1:2,000 is definitely a larger scale than 1:10,000 because these are fractions for which 1 being divided by
2,000 results in 0.0005, a number that is larger than 0.0001, which is the result of dividing 1 by 10,000.
•By data structure: In digital mapping, there are two basic data structures, rasters and vectors. Rasters are generally referred to as a collection of pixels. Each pixel is one single graphic data point. Much like in digital photography, the higher the number of pixels, the better the resolution or data representation. Aerial photographs, satellite images, and some elevation data are in a raster data structure. Vectors are data that are defined in a coordinate system that have x- and y- values in a two-dimensional plane or with z-values in a three-dimensional structure. X-, y-, z- values can all be continuous and can be represented in infinitely small numbers (many digits after the decimal). Each data point has a specific location in the coordinate system. Two data points make up a line (or an arc in GIS terms) and a minimum of three data points make up an area (polygon).
The vector data structure is very beneficial in a GIS because it allows GIS software to build a topology, a mathematic that computes the true and definable spatial relationship between data features. Topology is the fundamental part of an engine that drives the computerized spatial analysis and modeling routines in a GIS software program.
The raster-vector diagram illustrates the differences between raster and vector structures. While the raster structure is mainly used to represent satellite images and aerial photographs and does show some spatial relationship between features, the vector structure is a more efficient topological detector of spatial relationships. Imagine taking two points in a vector dataset; if a direction can be established between these points, it is then possible to identify certain relationships. From the vector diagram, assume that we take Point A as an origin (the “from-node” in GIS terminology) and Point E as a destination (the “tonode”), we can now calculate the distance and direction of travel from A to E. In addition, we can also describe Point K in relation to the direction of travel between A and E by acknowledging that K is to the right-hand side of the direction of travel. This simple routine is exactly how the U.S. Bureau of the Census can perform address-matching with its TIGER (Topologically Integrated Geographic Encoding Resources) software by identifying even or odd address numbers to the right or left. In the TIGER database, each street intersection is assigned a node, thus making it possible to pinpoint street addresses. By the same token, we can take any two points and join them as a line (or an arc in GIS terminology) or take any number of points and join them as an area (or a polygon in GIS terminology). In the raster-vector diagram, the shaded area ABCDEA is a closed area; thanks to the use of topology, we can definitively conclude that Point K is clearly contained in this area and Point J is clearly outside this area. If point, line, and area features can be located in space (based on a coordinate system), buffers can also be built to surround each feature. These buffers can be used to encompass other thematic features in a relational database. For example, TIGER can use the buffer to round up all the number of people who live within that specified buffer zone. If a river is determined to have a potential flooding of 100 feet from its banks, a linear buffer can be specified in a GIS to identify all the houses within the buffer that are prone to flooding. Thus, we can really see the benefits of performing spatial analysis and advanced spatial and statistical modeling using topological concepts. In addition, we can also add spatial layers to the GIS, thus providing us with a lot more flexibility and analytical power to perform spatial analysis across layers.
<drawing> Raster data structure
<drawing> Vector data structure