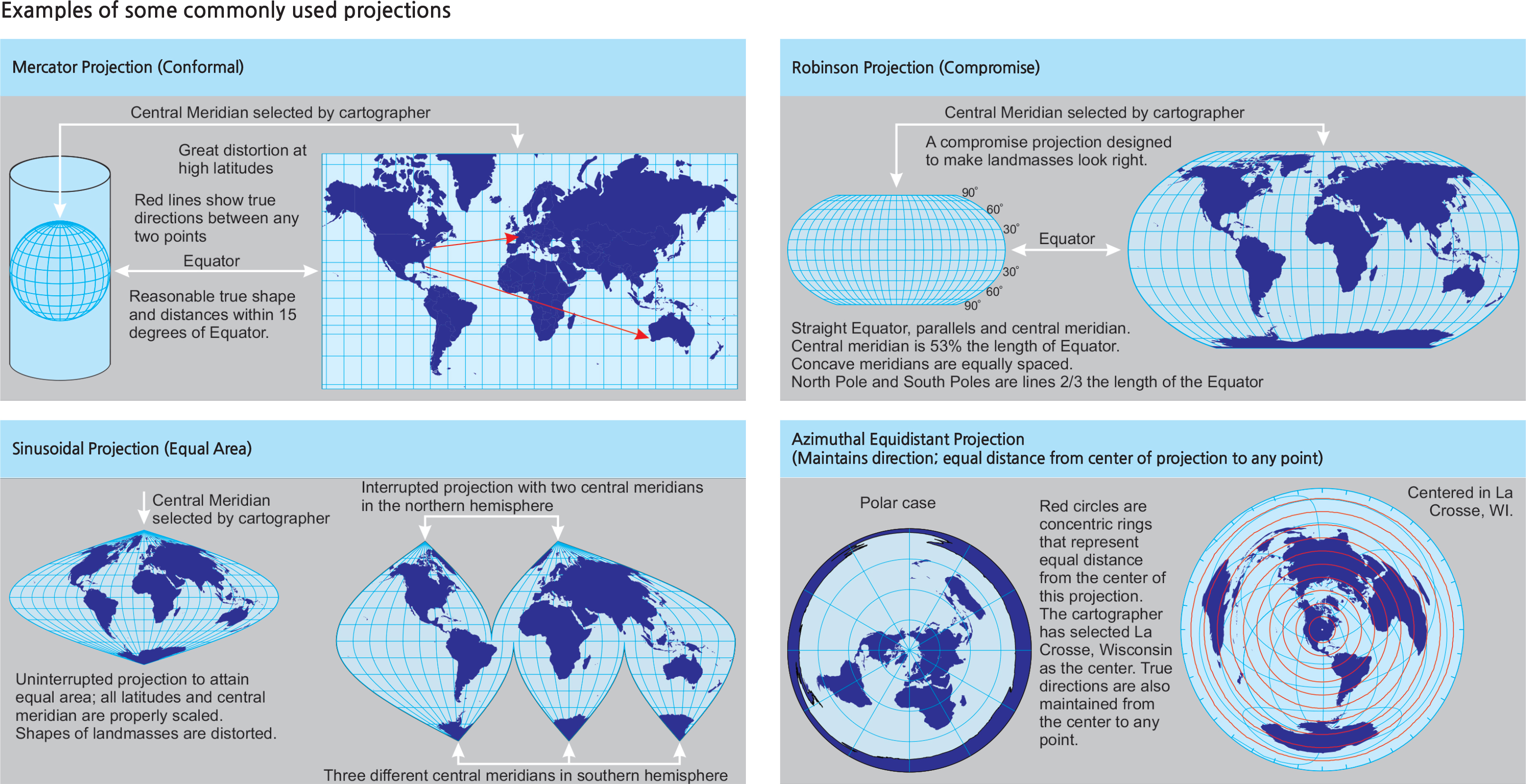
In order to have maps made accurately, cartographers need to know the exact shape of the earth. The axis between the North Pole and the South Pole is shorter than the axis between opposites ends of the Equator. No single mathematical formula can describe the shape of the earth because of the discrepancy between axes (due to the earth not being perfectly round) and because of the unique surface of the earth with uneven distribution and elevation of landmasses and oceans. Alexander Ross Clarke (1828- 1914), a British geodesist (a scientist who makes precise locational measurements of the surface of the earth) made measurements of the earth from many different locations around the world. His measurements were mathematically documented with a set of complex formulae and would become the foundation of The Clarke Spheroid of 1866 (a spheroid is a unique description of an imperfect sphere). The Clarke Spheroid became a very important set of mathematical descriptions of the shape of the earth for international cartographers and scientists to use. It was adopted by the U.S. Geological Survey as the basis for the 1927 North American Datum (NAD27) as a standard for producing U.S. topographic maps. In the case of the mapping sciences, the word “datum” is used to refer to a set of base information carefully measured and documented. This set of base information is used as a standard for measuring associated land. The 1927 North American Datum was the standard by which all land in the United States was referenced between 1927 and 1983. It consisted of a horizontal datum and a vertical datum. The horizontal datum began with an east-west stretch of flat land and a north-south stretch of flat land at Meade’s Ranch in Kansas, roughly the geographic center of the continental United States. Careful triangulations of these stretches of land were recorded. All land measurements in the continental U.S. are referenced to these triangulation results at Meade’s Ranch. The vertical datum was derived from over 35 years of measurements of variations in sea level to find the Mean Sea Level (MSL). The MSL then became the basis for measuring all elevations in the United States.

 Since the U.S. military’s 1983 declassification of Global Positioning Satellites (GPS) for the purpose of civilian use, geodesy (the science of precisely locating point positions on the surface of the earth) has greatly increased in accuracy over the 1927 North American Datum. The surface of the earth can now be “remapped” based on GPS methods. Thus, new datums are constantly evolving. In 1983, the World Geodetic Survey (WGS) started to use the WGS83 Datum, followed immediately by the WGS84 Datum. Subsequently, more datums were created, some to meet an individual country’s specific needs, others to define specific coordinate grid systems. Nevertheless, all these datums are mathematically documented so that transforming from one datum to another can be calculated. These calculations are normally embedded in GIS software and such calculations can be performed with a few strokes or clicks on the mouse. To learn more about datums, coordinate systems, and GPS, please read Chapters 1, 4, and 14 of Map Use (Kimerling 2016).

  Now that the measurement of the land surface has been accomplished, another problem needs to be addressed. Remember that a map is a transformation from the real, (not perfectly) round, three-dimensional world onto a twodimensional flat piece of paper or digital display surface. This transformation cannot occur without geometric error. This is where the understanding of map projections is important. Map projections make use of a network of coordinate systems or grids (the most popular one being The Geographic Coordinate System, which uses latitudes and longitudes) such that “casting” or “projecting” this network of grids onto a flat surface may allow us to document the amount of distortion introduced in every map projection transformation. Depending on the method used to cast latitude and longitude onto a flat surface, every resulting projection cannot accurately maintain both size and shape properties of the landmasses simultaneously. One or the other or both properties must be sacrificed. For this reason, there are equal-area map projections which maintain the truthfulness of area measurements at the expense of distorting the shape of landmasses. There are also conformal map projections that maintain the shape of the landmasses at the expense of distorting the truthfulness of area sizes. A mathematical or compromise map projection (by far the largest category) may sacrifice both area and shape properties to a lesser degree in order to present a more “realistic look” of the world’s landmasses. Most map projections which centered on the North and South Poles can maintain true directions. To learn more about map projections, please read Chapter 3 of Map Use (Kimerling 2016).